CALCOLO DELL’INFLESSIONE DELLE TRAVI IN C.A.
Una delle verifiche che la normativa impone per quanto riguarda gli SLE è quella di inflessione, da limitare opportunamente in funzione delle caratteristiche specifiche dell’edificio (estetica, funzionalità, presenza di tamponamenti fragili, etc…)
La verifica di inflessione delle travi in c.a., da eseguire a valle di quella a SLU, deve tener conto sostanzialmente dei fenomeni viscosi e della fessurazione del cls. Le formule della Scienza delle Costruzioni sono sempre valide, ma andranno opportunamente calibrate per tenere conto dei suddetti fenomeni, riducendo l’inerzia e il modulo elastico del cls.
La normativa fornisce una formulazione semplificata, che valuta sostanzialmente una curvatura “media” delle sezioni, che tiene conto del fenomeno di fessurazione del cls (stadio II) nonché del tension stiffening, ovvero il contributo di resistenza a trazione del cls nelle sezioni non fessurate (stadio I):
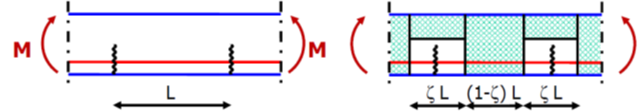
Il comportamento complessivo dell’elemento può essere dunque valutato come una sorta di “media pesata” delle curvature calcolate nei casi “estremi” di sezione fessurata e sezione interamente reagente:
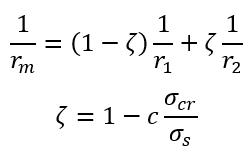
c è un coefficiente che tiene conto della durata del carico (1 per carichi di breve durata, 0.5 per carichi permanenti o ciclici)
σcr è il valore di tensione nell’acciaio calcolata nell’ipotesi di sezione fessurata sotto il carico che provoca la fessurazione
σs è la tensione effettiva nell’acciaio
Se il quantitativo di acciaio è costante lungo l’elemento e nell’ipotesi di comportamento elastico lineare dei materiali, le tensioni sono proporzionali ai rispettivi momenti:
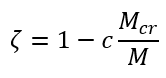
L’integrazione delle curvature è agevole nelle strutture isostatiche mentre risulta più complesso su quelle iperstatiche (operazione che viene effettuata da qualunque programma calcolo numerico, ma di difficile applicabilità “a mano” vista la necessità di effettuare un calcolo iterativo molto oneroso).
Le norme consentono dunque di valutare l’inflessione in modo semplificato attraverso la seguente espressione:
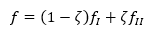
fI è la freccia corrispondente allo stadio I (sezione interamente reagente)
fII è la freccia corrispondente allo stadio II (sezione parzializzata)
La viscosità può essere tenuta in conto applicando il coefficiente viscoso φ(∞,t0) ad fI e considerando un modulo elastico ridotto Ec*=Ec/(1+ φ(∞,t0)) per il calcolo di fII.
ESEMPIO DI CALCOLO
Consideriamo una trave in semplice appoggio di lunghezza L=400 cm di sezione 25×40 cm armata con 4Ф16 +2 Ф14 – st. Ф8 – Acciaio B450C – cls C25/30 Copriferro c=3cm.
Avremo:
d = 40-3-0.8-0.7=35.5 cm
As = 8.04 cm2
A’s = 3.08 cm2
fyd= 3913 daN/cm2=391.3 MPa
fctm = 0.30∙fck2/3= 2.6 MPa = 26 daN/cm2
Per prima cosa occorrerà valutare il momento di fessurazione, cioè il momento flettente che fa raggiungere la tensione di trazione fctm nelle fibre di cls più tese.
Per velocizzare il calcolo del momento di fessurazione, facilmente calcolabile anche a mano con poche iterazioni, utilizziamo VCA SLU, utilizzando il metodo n (tensioni ammissibili) e attivando la resistenza a trazione del cls e la visualizzazione delle tensioni nel cls (troviamo iterativamente il valore di momento che comporta una tensione di 2.6 MPa in intradosso:
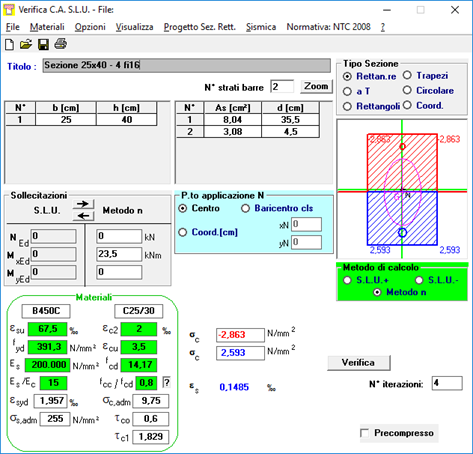
Mcr = 20.5 kNm = 205000 daN∙cm
Per la valutazione del momento in combinazione QP utilizziamo i seguenti carichi (ipotizzando una fascia di carico i=3.00 m):
p.p. = 315 daN/m2
permanenti = 250 daN/m2
variabili = 200 daN/m2 (Cat. A – ψ2,1=0.3)
Da cui:
MQP = 42.5 kNm = 425000 daN∙cm
Per la valutazione della profondità dell’asse neutro x si eguaglia a 0 il momento statico:
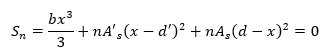
Da cui si ricava:
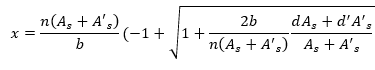
Nota la posizione dell’asse neutro, il momento d’inerzia della sezione fessurata vale dunque:
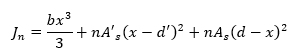
L’equazione del momento statico può essere risolta numericamente impostando il tutto in un foglio di calcolo e impiegando la funzione “ricerca obiettivo”.
Nel caso in esame, risulta x=13.17 cm e Jn=83703,34 cm4.
Calcoliamo le frecce a tempo infinito (stadio I e stadio II):
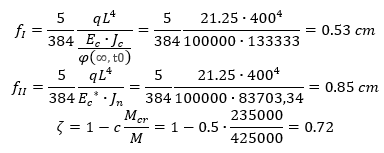
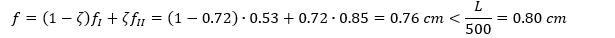
La verifica è soddisfatta e tutti i calcoli sono riportati nella tabella seguente, implementata su un foglio di calcolo Excel.
| Verifica di inflessione nelle travi in c.a. rettangolari | |||
| Dati Geometrici della sezione | |||
| Base | b | 25,00 | [cm] |
| Altezza | h | 40,00 | [cm] |
| Distanza tra bordo compresso e armature compresse | d’ | 4,50 | [cm] |
| Altezza utile | d | 35,50 | [cm] |
| Area sezione | A | 1000,00 | [cm2] |
| Momento d’inerzia | Jx | 133333,33 | [cm4] |
| Modulo di resistenza | Wx | 6666,67 | [cm3] |
| Area acciaio teso | As | 8,04 | [cm2] |
| Area acciaio compresso | A’s | 4,02 | [cm2] |
| Modulo elastico acciaio | Es | 2100000 | [daN/cm2] |
| Modulo elastico cls | Ec | 300000 | [daN/cm2] |
| Coeff. di viscosità | φ(∞,t0) | 2,00 | [-] |
| Modulo elastico cls ridotto | Ec* | 100000,00 | [daN/cm2] |
| Coeff. di omogeneizzazione | n | 15 | [-] |
| Schema di carico (Combinazione S.L.E.) | |||
| Lunghezza | L | 400,0 | [cm] |
| Peso proprio e permanenti | G | 1945,0 | [daN/m] |
| Carico variabile | Q | 600,0 | [daN/m] |
| Coeff. di combinaz. | ψjk | 0,3 | [-] |
| Coefficiente di vincolo a momento | 8 | [-] | |
| Carico totale | q | 2125,0 | [daN/m] |
| Momento flettente in campata | MSLE | 425000,0 | [daN·cm] |
| Momento di fessurazione | Mcr | 235000,0 | [daN·cm] |
| Caratteristiche sezione fessurata | |||
| Posizione asse neutro | x | 13,17 | [cm] |
| Momento statico | Sn | 0,00 | [cm3] |
| Momento d’inerzia | Jn | 83703,34 | [cm4] |
| Calcolo inflessioni | |||
| Coefficiente di vincolo per deformazioni | 5/384 | [-] | |
| Inflessione di stadio I | fI | 0,53 | [cm] |
| Inflessione di stadio II | fII | 0,85 | [cm] |
| Coefficiente di durata | c | 0,5 | [cm] |
| ζ | 0,72 | ||
| Inflessione totale | f | 0,76 | [cm] |
| f< L/500 | 0,80 | [cm] |
Ovviamente, si è dato per scontato che le verifiche di SLU fossero già soddisfatte.
Per completezza, un valore orientativo di momento resistente a SLU della sezione in oggetto può essere calcolato in accordo a quanto spiegato nel precedente articolo:
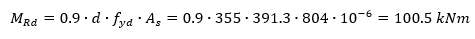
e confermato da VCA SLU:
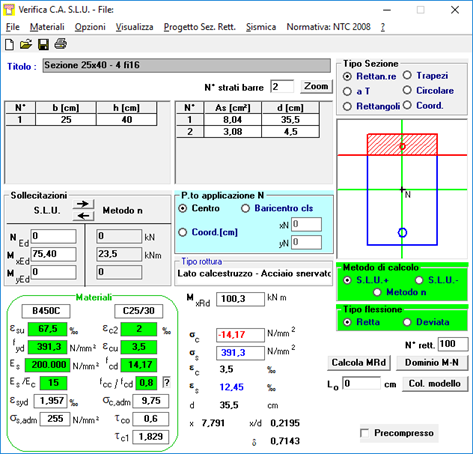
Da confrontare con il valore di momento agente a SLU MEd = 75.4 kNm.

No responses yet